How Do You Know if a Line Is Slanting Down
Horizontal and Vertical Lines
Permit's consider again the two equations nosotros did first on the previous page, and compare the lines' equations with their slope values.
The beginning line'due south equation was , and the line's slope was .
The second line's equation was y = –2 10 + iii, and the line'due south slope was m = –2 .
In both cases, the number multiplied on the variable x was also the value of the slope for that line. This relationship always holds true: If the line's equation is in the course " y=", then the number multiplied on x is the value of the slope grand .
Content Continues Beneath
This relationship will become very important when you start working with directly-line equations.
At present permit'south consider those two equations and their graphs.
For the first equation, , the slope was , a positive number. The graph looked like this:
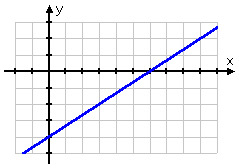
Notice how the line, as we move from left to correct along the 10 -axis, is edging upward toward the top of the drawing; technically, the line is an "increasing" line. And... the slope was positive.
This relationship always holds truthful: If a line is increasing, so its slope will be positive; and if a line's slope is positive, then its graph will be increasing.
For the second line, y = –iix + 3, the slope was 1000 = –2, a negative number. The graph looked like this:

Notice how the line, equally we move from left to correct forth the x -axis, is edging downward toward the lesser of the drawing; technically, the line is a "decreasing" line. And... the slope was negative.
This relationship is always truthful: If a line is decreasing, then its slope will be negative; and if a line'due south slope is negative, then its graph will be decreasing.
This relationship betwixt the sign on the gradient and the direction of the line's graph can help you check your calculations: if you calculate a gradient as being negative, but you tin see from the graph of the equation that the line is actually increasing (and then the gradient must be positive), and then y'all know you need to re-do your calculations. Being aware of this connection tin salve you points on a test because information technology will enable you to check your work earlier y'all hand it in.
So now we know: Increasing lines accept positive slopes, and decreasing lines take negative slopes. With this in mind, let's consider the following horizontal line:
y = 4
Its graph is shown below:
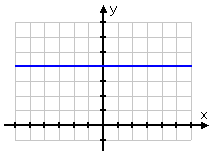
Is the horizontal line edging upward; that is, is it an increasing line? No, so its slope can't be positive. Is the horizontal line edging downwardly; that is, is information technology a decreasing line? No, so its slope can't exist negative. What number is neither positive nor negative?
Goose egg!
So the gradient of this (and any other) horizontal line should, logically, exist nada. Let's do the calculations to ostend this. Using the (arbitrary) points from the line, (–3, 4) and (five, 4), the gradient computes every bit:
This human relationship e'er holds: a gradient of zero means that the line is horizontal, and a horizontal line ways you'll get a slope of zero.
(By the way, all horizontal lines are of the grade " y = some number", and the equation " y = some number" always graphs equally a horizontal line.)
At present consider the following vertical line:
10 = 4
Its graph is below.
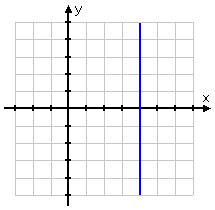
Is the vertical line going up on one terminate? Well, yes, kind of. So maybe the slope will exist positive...? Is the vertical line going down on the other finish? Well, over again, kind of. So possibly the slope will be negative...?
But is at that place whatsoever number that is both positive and negative? Nope.
Verdict: vertical lines take NO Gradient. The concept of slope simply does not piece of work for vertical lines. The slope of a vertical line does not exist!
Let's do the calculations to confirm the logic. From the line'south graph, I'll utilize the (arbitrary) points (4, 5) and (4, –3). And so the gradient is:
We tin can't divide by zero, which is of grade why this slope value is "undefined".
This relationship is ever true: a vertical line will take no gradient, and "the gradient is undefined" or "the line has no slope" ways that the line is vertical.
(By the mode, all vertical lines are of the class " 10 = some number", and " x = some number" means the line is vertical. Any fourth dimension your line involves an undefined gradient, the line is vertical; and any time the line is vertical, yous'll end upwardly dividing past nothing if y'all try to compute the slope.)
Warning: It is very common to confuse these 2 types of lines and their slopes, but they are very different.
Merely equally "horizontal" is non at all the aforementioned as "vertical", and then also "zero gradient" is non at all the same as "no slope".
But as a "Z" (with its 2 horizontal lines) is non the same every bit an "N" (with its ii vertical lines), so as well "Nothing" gradient (for a horizontal line) is not the same as "No" slope (for a vertical line).
The number "null" exists, so horizontal lines practice indeed have a slope. But vertical lines don't have any gradient; "slope" simply doesn't take whatsoever meaning for vertical lines.
It is very common for tests to contain questions regarding horizontals and verticals. Don't mix them up!
Source: https://www.purplemath.com/modules/slope2.htm
0 Response to "How Do You Know if a Line Is Slanting Down"
Post a Comment